근의 공식의 쓸모
근의 공식은 $ax^2 + bx + c = 0$ 형식의 이차 방정식을 푸는 데 유용한 도구입니다.
근의 공식을 통해 방정식을 만족하는 $x$의 값을 찾을 수 있습니다.
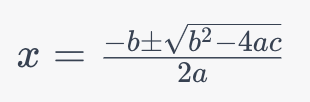
우리는 이차방정식의 근이나 해를 구하고자 할 때 근의 공식을 사용합니다. 근은 이차 방정식이 $x$축과 교차하는 $x$값을 나타냅니다.
근의 공식의 유도
근의 공식을 유도하기 위해 일반적인 이차 방정식 $ax^2 + bx + c = 0$부터 시작합니다.
이차 방정식을 유도하는 단계는 다음과 같습니다.
방정식 $ax^2 + bx + c = 0$로 시작합니다.
방정식을 $a$로 나누면 $x^2$의 계수는 $1$가 됩니다
$x^2 + \frac{b}{a}x + \frac{c}{a} = 0$.
상수 항 $\left(\frac{c}{a}\right)$를 방정식의 오른쪽으로 이동합니다.
$x^2 + \frac{b}{a}x = -\frac{c }{a}$.
제곱을 완성하려면 $x$ 계수의 절반을 취하여 제곱하고 방정식의 양쪽에 더합니다. 왼쪽은 완전제곱식 삼항식이 됩니다
$x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)^2 = -\frac{c}{a} + \left(\frac{b}{2a}\right)^2$.
방정식을 단순화합니다
$\left(x + \frac{b}{2a}\right)^2 = \frac{b^2 - 4ac}{4a^2}$.
양변에 제곱근을 취합니다
$x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 - 4ac}}{2a}$.
마지막으로 양쪽에서 $\frac{b}{2a}$를 빼서 $x$를 분리합니다
$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$.
근의 공식과 근의 특징
- 두 근: 이차 공식은 $x_1$ 및 $x_2$로 표시되는 $x$의 두 가지 가능한 값을 제공합니다. 이들은 방정식이 $x$축과 교차하는 $x$값을 나타내는 이차 방정식의 근입니다.
- 판별식: 제곱근 $b^2 - 4ac$ 아래의 식을 판별식이라고 합니다. 근의 특성을 결정하고 이차 방정식의 해에 대한 정보를 제공합니다.
- 판별식이 양수이면($b^2 - 4ac > 0$) 방정식에는 두 개의 고유한 실근이 있습니다. 이것은 이차 그래프가 두 개의 다른 지점에서 $x$ 축과 교차한다는 것을 의미합니다.
- 판별식이 0이면($b^2 - 4ac = 0$) 방정식의 실근은 하나입니다. 이것은 2차 그래프가 단일 점(정점)에서 $x$축에 닿는다는 것을 의미합니다.
- 판별식이 음수이면($b^2 - 4ac < 0$) 방정식에 실근이 없습니다. 이것은 2차 그래프가 $x$ 축과 교차하지 않고 해가 복소수 또는 허수임을 의미합니다.
근의 공식의 역사
근의 공식이라고도 하는 이차 공식은 수세기 동안 알려지고 사용되었습니다. 그 발견을 한 개인에게 돌리는 것은 어렵습니다. 고대 바빌로니아인, 이집트인, 그리스인은 이차방정식을 푸는 방법을 가지고 있었지만 그들의 접근 방식은 오늘날 우리가 사용하는 이차방정식만큼 대수적이지는 않았습니다.
공식적인 표현의 관점에서 오늘날 우리가 알고 있는 이차 공식은 페르시아의 수학자이자 천문학자인 Al-Khwarizmi(c. 780-850)까지 거슬러 올라갈 수 있습니다. Al-Khwarizmi는 그의 영향력 있는 저서 "Kitab al-Jabr wal-Muqabala"(완성 및 균형에 의한 계산에 관한 Compendious Book)에서 본질적으로 2차 공식인 것을 사용하여 2차 방정식을 푸는 체계적인 방법을 제공했습니다.
그러나 2차 공식이 Al-Khwarizmi에 의해서만 발견된 것은 아니라는 점에 유의하는 것이 중요합니다. 이 공식은 다른 문화와 시대의 다양한 수학자들의 기여를 통해 시간이 지남에 따라 진화했을 가능성이 높습니다. 여기에는 인도 수학자, 중국 수학자, 이슬람 황금 시대 학자 등이 포함됩니다.
전반적으로 이차 공식의 발전은 역사를 통틀어 수학자들의 집단적 노력의 결과입니다.
'궁금증 해결 > 이과적궁금증' 카테고리의 다른 글
| 편미분이란? 편미분의 역사, 편미분 관련 주요 정의, 편미분의 활용분야 (0) | 2023.06.18 |
|---|---|
| 테일러 급수란? 테일러급수의 용도, 증명, 역사 (1) | 2023.06.06 |
| 세상에서 가장 아름다운 공식 - 오일러 항등식을 테일러급수로 증명 (0) | 2023.05.16 |
| ChatGPT 답변이 중간에 끊길때 해결방법 - "계속해" (1) | 2023.05.10 |
| ChatGPT 끼리 소개팅을 시킨다면? 대환장 파티 오픈. 시키는 대로 좀 해줘 ㅠㅠ (1) | 2023.05.10 |



