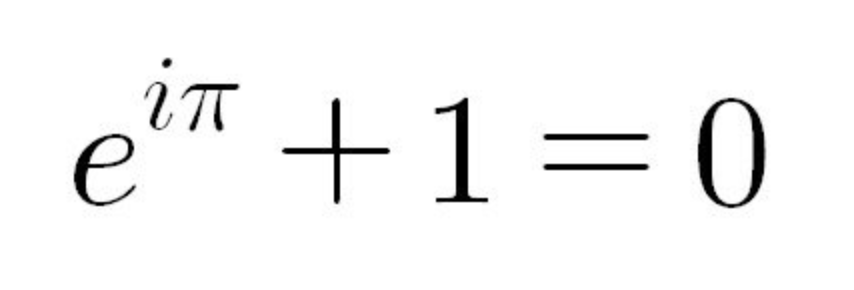
오일러 항등식
오일러의 항등식을 증명하려면 복소 지수 표현과 오일러 공식에 대한 이해가 필요합니다.
오일러의 항등식은 다음과 같습니다:
e^(iπ) + 1 = 0
여기서 e는 자연로그의 밑이며, i는 허수 단위이고, π는 원주율입니다.
이 항등식을 증명하기 위해, 먼저 오일러의 공식인 e^(ix) = cos(x) + i*sin(x)를 사용합니다. 이 식은 오일러가 발견한 중요한 결과로, 실수 x에 대한 복소 지수 함수와 삼각 함수 사이의 관계를 보여줍니다.
이제 오일러의 공식을 사용하여 오일러의 항등식을 증명해 보겠습니다:
e^(iπ) + 1 = cos(π) + i*sin(π) + 1
cos(π)는 -1이고, sin(π)는 0입니다. 따라서 다음과 같이 정리할 수 있습니다:
e^(iπ) + 1 = -1 + i*0 + 1
이를 간소화하면 다음과 같이 됩니다:
e^(iπ) + 1 = 0
테일러급수란?
테일러 급수는 함수를 무한히 많은 항들로 근사하는 방법입니다. 함수 f(x)의 테일러 급수는 다음과 같이 나타낼 수 있습니다:
f(x) = f(a) + f'(a)(x-a)/1! + f''(a)(x-a)^2/2! + f'''(a)(x-a)^3/3! + ...
여기서 f'(a)는 f(x)의 a에서의 미분계수(1차 미분)를 의미하며, f''(a)는 f(x)의 a에서의 2차 미분계수를 의미합니다.
a는 근사를 하고자 하는 지점입니다.
테일러 급수를 활용한 오일러 공식의 증명
오일러의 항등식을 증명하기 위해선, 테일러 급수를 사용하여 e^x, sin(x), cos(x)를 근사하는 방법을 이용합니다.
e^x의 테일러 급수는 다음과 같이 표현됩니다:
e^x = 1 + x/1! + x^2/2! + x^3/3! + ...
sin(x)의 테일러 급수는 다음과 같이 표현됩니다:
sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ...
cos(x)의 테일러 급수는 다음과 같이 표현됩니다:
cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ...
이제 오일러의 항등식을 증명해 보겠습니다:
e^(ix) = 1 + ix/1! - x^2/2! - ix^3/3! + x^4/4! + ...
cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ...
sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ...
여기서 x를 π로 대체해 보면:
e^(iπ) = 1 + iπ/1! - (π^2)/2! - i(π^3)/3! + (π^4)/4! + ...
cos(π) = 1 - (π^2)/2! + (π^4)/4! - (π^6)/6! + ...
sin(π) = π - (π^3)/3! + (π^5)/5! - (π^7)/7! + ...
이제 위의 테일러 급수들을 계산하면 다음과 같습니다:
e^(iπ) = 1 + iπ/1! - (π^2)/2! - i(π^3)/3! + (π^4)/4! + ...
cos(π) = -1 + 1/2! - 0 + 0 - ...
sin(π) = 0 - π^3/3! + 0
이제 식을 단순화해 보겠습니다:
e^(iπ) = 1 + iπ - π^2/2! - iπ^3/3! + π^4/4! + ...
cos(π) = -1 + 1/2! - 0 + 0 - ...
sin(π) = 0 - π^3/3! + 0 + ...
항을 재배열하여 e^(iπ)를 다음과 같이 다시 쓸 수 있습니다:
e^(iπ) = (1 - π^2/2! + π^4/4! - ...) + i(π - π^3/3! + π^5/5! - ...)
이제 괄호 안의 항을 살펴보면, 이들은 각각 코사인과 사인의 테일러 급수 확장과 유사함을 알 수 있습니다.
따라서 식을 다음과 같이 다시 쓸 수 있습니다:
e^(iπ) = cos(π) + i*sin(π)
cos(π)가 -1이고, sin(π)가 0이므로 다음과 같습니다:
e^(iπ) = -1 + i*0
더 단순화하면:
e^(iπ) = -1
양변에 1을 더하면:
e^(iπ) + 1 = 0
따라서 지수 함수, 코사인 함수, 사인 함수의 테일러 급수 확장을 사용하여 오일러의 항등식을 증명하였습니다.
'궁금증 해결 > 이과적궁금증' 카테고리의 다른 글
| 테일러 급수란? 테일러급수의 용도, 증명, 역사 (1) | 2023.06.06 |
|---|---|
| 근의 공식, 근의 공식 유도, 판별식, 근의 공식의 역사 - 이차방정식의 해를 구하고 해의 성질을 알려주는 근의공식 (0) | 2023.05.27 |
| ChatGPT 답변이 중간에 끊길때 해결방법 - "계속해" (1) | 2023.05.10 |
| ChatGPT 끼리 소개팅을 시킨다면? 대환장 파티 오픈. 시키는 대로 좀 해줘 ㅠㅠ (1) | 2023.05.10 |
| chatGPT 에 뭘 어떻게 물어봐야 할지 모르겠다면? chat GPT 명령어 샘플 120가지 (0) | 2023.05.09 |



