알고리즘 문제를 풀다보면 big-O notation을 통해 시간복잡도, 공간복잡도를 계산하곤 합니다.
저는 대략적인 호출 수, for loop, 캐싱 등을 염두에 두고 계산하곤 했는데요,
CTCI(Cracking the Code Interview)책을 읽다 보니 recursion, string, binary tree 등에서 보다 정확한 Big-O Notation에 대한 부분이 있어 정리해두려고 합니다.
01. big-O 표기법이란?
big-O 표기법은 N에 따라 수행시간이 어떻게 변화하는지를 표현해주는 도구입니다.
두 big-O 표기법 중 어떤게 더 수행시간이 빠른지를 비교하는것이 아닙니다!
즉, big-o 표기로 더 크다고 해서 항상 더 느린 것은 아닙니다.
입력과 연산에 따라 O(N) 코드가 O(1) 코드보다 더 빠르게 동작하는 경우도 있습니다.
(수행시간을 정확히 이해하려면 컴퓨터 단에서 실행되는 명령어의 갯수를 직접 파악해야 합니다. 예를들어 어셈플리 단계에서 곱셈이 덧셈보다 더 많은 명령어를 사용한다는 점, 컴파일러가 나름의 최적화를 한다는 점 등등 모든 세부사항을 고려해야 하는데, 이런 작업은 매우 복잡하죠.)
02. 기본원칙
1. 상수항은 무시
O(2N) -> O(N)으로만 표기
2. 지배적이지 않은 항은 무시
O(N^2 + N) -> O(N^2)으로만 표기
아래로 갈수록 더 지배적인 항입니다.
| O(1) |
| O(logN) |
| O(N) |
| O(NlogN) |
| O(N^2) |
| O(2^N) |
| O(N!) |
03. 배열의 삽입 : O(1)
크기가 자유롭게 조절되는 배열(ex) ArrayList)는 처음 선언시 임의의 크기로 공간을 할당하고, 그 크기를 넘어가면 그 크기의 두배만큼을 할당합니다.
1. 배열에 N개보다 작은 원소가 들어있으면 남은 자리에 새 원소를 삽입 O(1)
2. 배열에 N개 원소가 들어있으면 크기가 2N인 배열을 새로 만들고 기존의 모든 원소를 새 배열로 복사한 후 삽입 O(N)
배열의 크기를 두배로 늘리는 연산(O(N))은 배열의 크기가 1, 2, 4, 8, 16.. 등 2의 승수일 때 일어납니다.
즉, X개의 원소를 삽입했을 때, 원소의 갯수에 따른 수행시간은 아래 표와 같아집니다.
| 원소의 갯수 | 수행시간 |
| X | O(X) |
| X-1 | 1 |
| X-2 | 1 |
| ... | |
| X/2 | O(X/2) |
| X/2 -1 | 1 |
| X/2 -2 | 1 |
| ... | |
전체 수행시간을 계산해보면
O(X) + O(X/2) + O(X/4) ... +1 = O(2X)
책에는 없었지만 수행시간이 1인 항들은 총 X-logX 개 일 거고 이 부분의 수행시간은 총 O(X) 가 될 것입니다.
이제, 평균적인 수행시간을 생각해보겠습니다.
전체 수행시간을 전체 원소의 갯수 X로 나눠 평균 수행시간을 구하면 O(1)이 됩니다.
04. 재귀함수 : O(분기^깊이)
재귀함수의 big-O 계산은 문제풀 때도 헷갈렷던 부분인데요,
일반적으로 재귀함수에서 수행시간은 O(분기^깊이)로 표현합니다.
ex 1) 분기가 2이므로 O(2^N)이 된다.
inf f(int n)
if(n<=1) {
return 1;
}
return f(n-1) + f(n-1);
}실제로 호출된 횟수를 그려보면, 아래 그림과 같은 트리 형태가 되겠죠
이 때 전체 노드의 수는 2^0 + 2^1 + 2^2 + 2^3 ... + 2^N= 2^(N+1)-1 이 됩니다.
이를 big-o로 표현하면 O( 2^(N+1)-1 ) = O( 2* 2^N-1 ) = O( 2^N )

이 알고리즘의 공간복잡도는 O(N)입니다.
공간복잡도를 확인하려면 알고리즘의 call stack이 어떤 모습일지를 생각해보면 되는데요,
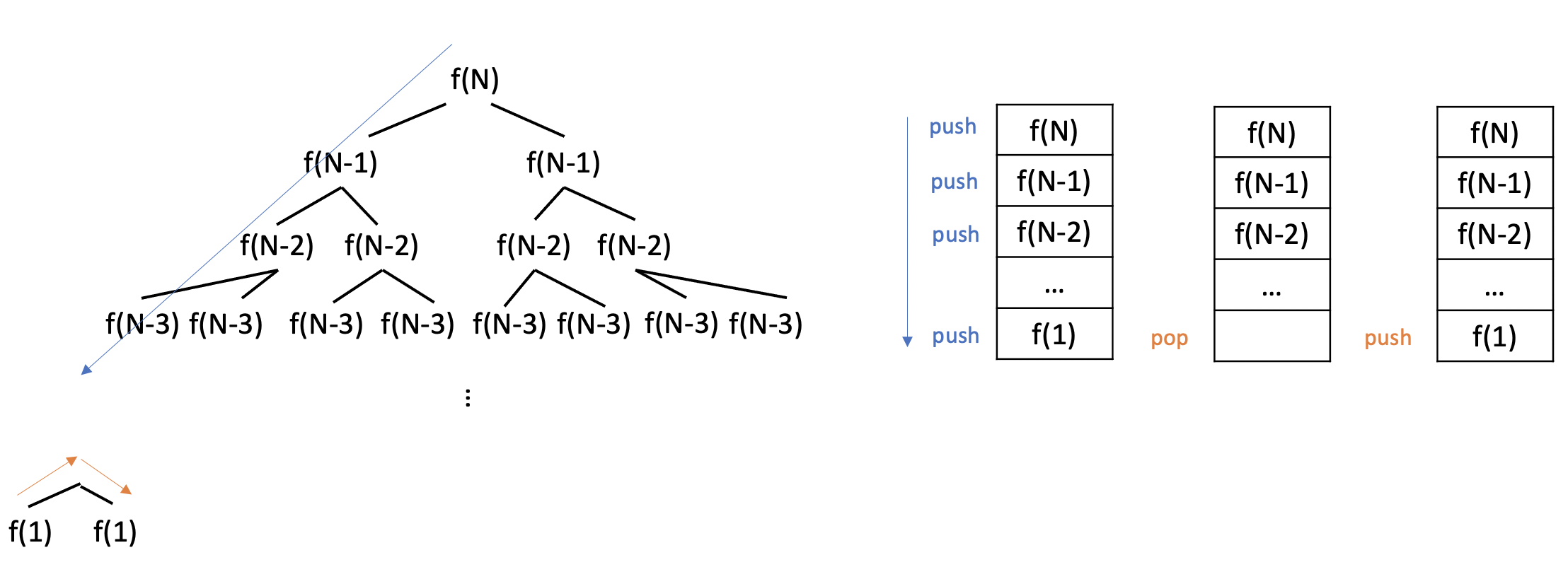
f(1)까지 다 계산한 후에는 call stack을 pop하고 다시 옆의 경로를 따라 call stack을 쌓겠죠.
따라서 N보다 큰 공간이 필요하지는 않습니다.
05. 이진트리의 순회 : O(N)
총 노드의 수가 N인 이진트리를 순회한다면 시간복잡도는 O(N)이 됩니다.
총 노드의 수가 N인 이진트리의 높이는 logN일거고, 트리의 분기는 2 입니다.
재귀함수에서와 같이 O(분기^높이) 에 따라 구해보면,
O(2^logN) = O(N)이 됩니다.

'알고리즘' 카테고리의 다른 글
| ALGOSPOT 문제 풀이 기록 (0) | 2017.10.23 |
|---|---|
| algospot :: ARCTIC 남극기지 (0) | 2017.10.23 |
| algospot :: DARPA DARPA Grand Challenge (0) | 2017.10.22 |
| algospot :: ALLERGY 알러지가 심한 친구들 (0) | 2017.10.22 |
| algospot :: BOARDCOVER2 게임판 덮기 2 (0) | 2017.10.21 |