Longest Palindromic Substring | LeetCode 780 | Python3 🐍

 

📄 목차

 

🤔 문제 : Longest Palindromic Substring | LeetCode 780

문제: https://leetcode.com/explore/interview/card/top-interview-questions-medium/103/array-and-strings/780/
palindorme : 거꾸로 읽어도 제대로 읽는 것과 같은 문장이나 낱말, 숫자, 문자열(sequence of characters) 

주어진 문자열에서 가장 긴 palindrome을 찾는 문제입니다.

palindrome은 항상 홀수 palindrome 짝수 palindrome 두가지 케이스 모두 고려해야 합니다.!

홀수 palindrome: babad

짝수 palindrome: cbbd

 

💡 풀이

1. 문자열을 순회하며 해당 문자를 중간문자로 하는 가장 긴 palindrome 찾기

가장 처음으로 접근한 풀이입니다. 

특정 문자를 중심으로 가장 긴 palindrome을 찾는 getPalindrome이라는 함수를 만들었고,

주어진 문자열을 순회하며 palindrome을 호출했습니다.

 

부분문자열(substring)을 다루는 함수를 만들 때는,

문자열을 직접 만들어서 전달하는 것 보다 index만 주고받는게 훨씬 빠릅니다.

 

from typing import List
class Solution:
    def longestPalindrome(self, s: str) -> str:
        str_length = len(s)

        def getPalindrome(idx1, idx2):
            if idx1 < 0: return (idx1, idx2)
            if idx2 >= str_length: return (idx1, idx2)
            if s[idx1] is not s[idx2]: return (idx1, idx2)
            return getPalindrome(idx1-1, idx2+1)

        longest_palindrome_size = 0
        longest_palindrome_pair = None
        for idx in range(str_length):		# [1] 
            (st, ed) = getPalindrome(idx, idx) # [2]
            if ed-st-1 > longest_palindrome_size:
                longest_palindrome_pair = (st, ed)
                longest_palindrome_size = ed-st-1

            (st, ed) = getPalindrome(idx, idx+1) # [3]
            if ed-st-1 > longest_palindrome_size:
                longest_palindrome_pair = (st, ed)
                longest_palindrome_size = ed-st-1

        return s[longest_palindrome_pair[0]+1:longest_palindrome_pair[1]]

[1]  idx번째 문자를 기준으로 palindrome을 찾을 것 

[2] 홀수 palindrome  ex) cabad

[3] 짝수 palindrome ex) cabbad

 

Time Complexity
문자열의 각 character에 대해(n) palindrome인지 여부를 확인하므로 (n)
O(n^2) 입니다. 

Space Complexity
별도 공간을 사용하지 않습니다.

 

 

 

2. 1의 풀이를 문자열을 만드는 방식으로 구현한 경우

문자열을 만들어 전달하는 방식으로 구현한 코드입니다.

Runtime이 5077ms으로 5배가량 오래 걸리네요.

class Solution:
    def longestPalindrome(self, s: str) -> str:
        str_length = len(s)

        def palindrome(idx1, idx2, curr_str):
            if idx1 is idx2: return palindrome(idx1-1, idx2+1, curr_str+s[idx1])
            if idx1 < 0: return curr_str
            if idx2 >= str_length: return curr_str
            if s[idx1] is not s[idx2]: return curr_str
            return palindrome(idx1-1, idx2+1, s[idx1]+curr_str+s[idx2])

        longest_palindrome = ""
        for idx in range(str_length):
            new_palindrome = palindrome(idx, idx, "")
            longest_palindrome = new_palindrome if len(longest_palindrome) <  len(new_palindrome) else longest_palindrome
            new_palindrome = palindrome(idx, idx+1, "")
            longest_palindrome = new_palindrome if len(longest_palindrome) <  len(new_palindrome) else longest_palindrome
        return longest_palindrome

 

3. dynamic programming

두 인덱스 사이의 substring이 palindrome인지 여부를 2차원 배열(cache)에 따로 저장해두는 방식입니다.

dabac 의 경우 cache모습이 아래와 같겠네요.

	d	a	b	a	c
d	1	0	0	0	0
a		1	0	1	0
b			1	0	0
a				1	0
c					1

cache의 값을 채우는 로직은 아래와 같습니다.

• 대각선 요소는 모두 1 
• 대각선 왼쪽 아래 요소가1이고 (시작, 끝 문자열 제외 palindrome)
  현재 가로축과 세로축의 문자가 같다면 시작, 끝 문자가 같음) 1 
• 나머지는 0

    def longestPalindrome(self, s: str) -> str:
        n = len(s)
        if n is 1: return s
    
        cache = [[0] * n for _ in range(n)]
        maxLength = 1
        longest_index_pair = (0,0)
    
        for i in range(n):
            cache[i][i] = 1
    
        for i in range(n-1):
            if s[i] is s[i+1]:
                if maxLength < 2:
                    maxLength = 2
                    longest_index_pair = (i, i+1)
                cache[i][i+1] = 1
    
        for i in range(2, n):
            for j in range(n-i):
                x = j
                y = j+i
    
                if s[x] is s[y] and cache[x+1][y-1]:
                    cache[x][y] = 1
                    if maxLength < i+1:
                        maxLength = i+1
                        longest_index_pair = (x, y)
        return s[longest_index_pair[0]:longest_index_pair[1]+1]

 

 

Time Complexity
O(N^2)

Space Complexity 
O(N^2)

 

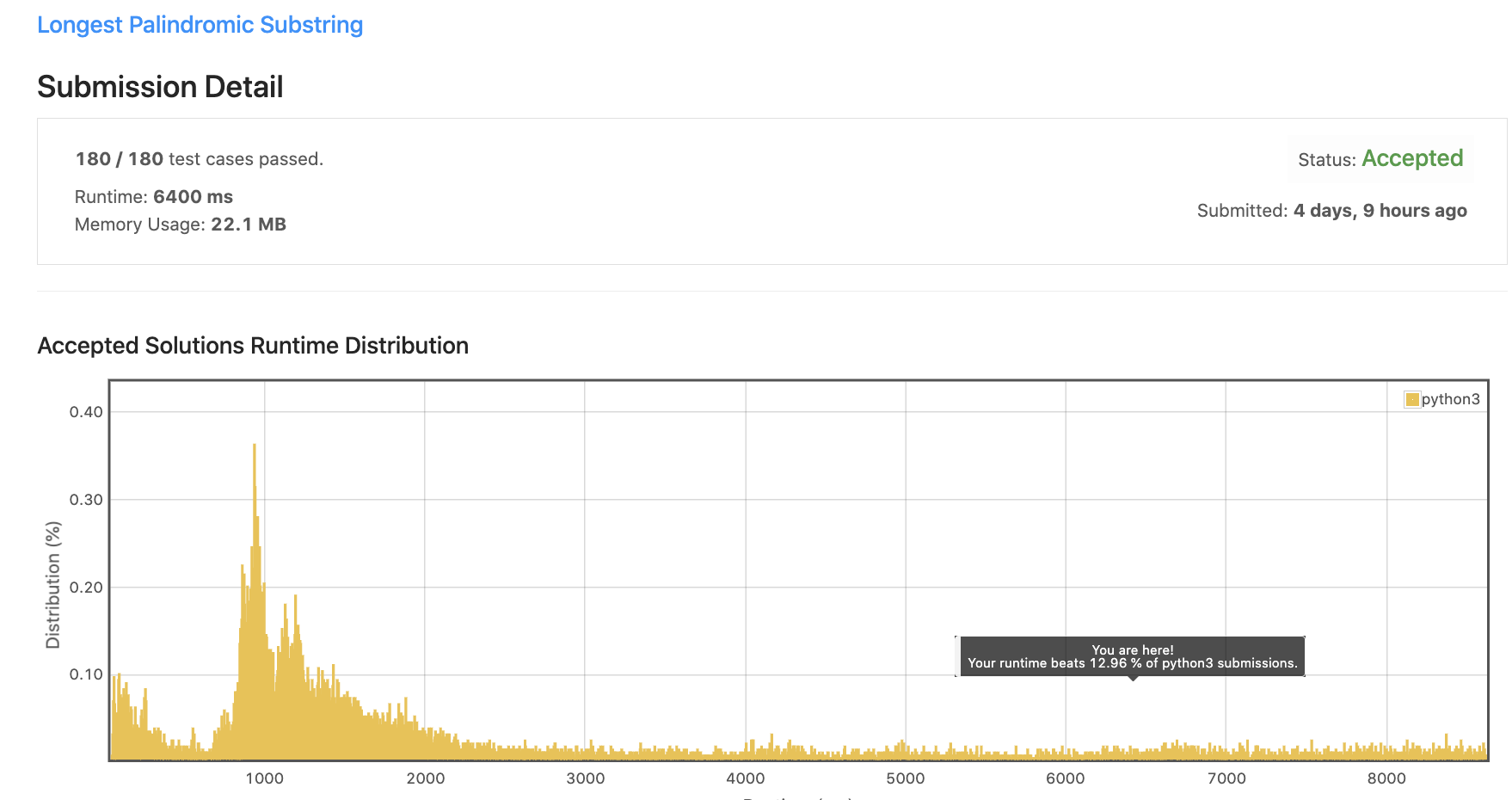
Time Complexity가 똑같이 N^2인 1번 풀이에 비해 수행시간이 훨씬 오래걸리네요.

아무래도 중간에 palindrome이 아닌게 확실한 케이스라도 전체를 다 보기 때문인 것 같습니다.

1은 worst case가 N^2이였다면, 이 풀이는 무조건 N^2인 거죠

 

 

4. 더 빠르게 - 연속된 문자열이 나올 경우 palindrome확인 없이 skip

다른 풀이가 있을까 discussion을 보다가 알게된 풀이인데, 간단하고 참신하여 같이 소개합니다.

 

이 풀이는 같은 문자가 연속해서 나올 경우에는 다 스킵하는 방식입니다.

생각해보면, 같은 문자가 연속해서 나온다면 좌우를 1:1로 굳이 비교할 필요가 없겠죠.

worst case(같은 문자가 연속해서 나오지 않는 경우)는 N^2으로 같겠지만, 평균 수행속도는 빨라지겠네요.

    # expand same characters
    def longestPalindrome(self, s: str) -> str:
        """
        The longest Palindrome including s[i] should contains substr s[l+1, r],
		where all elements in s[l+1, r] are s[i]
		This saves checks when a same char is repeated consecutively in s.
		"""
        p, idx = '', 0
        while idx < len(s):
			l = r = idx
			# expand when having same ajacent chars
			while l-1>=0 and s[l] == s[l-1]: l -= 1
			while r+1<len(s) and s[r] == s[r+1]: r+=1
			idx = r+1 # update idx, this can save checks
    
			# expand to different chars
			while l>=0 and r<len(s) and s[l] == s[r]:
				l, r = l-1, r+1
			# update p
			p = max([p, s[l+1:r]], key = lambda x:len(x))
    
		return p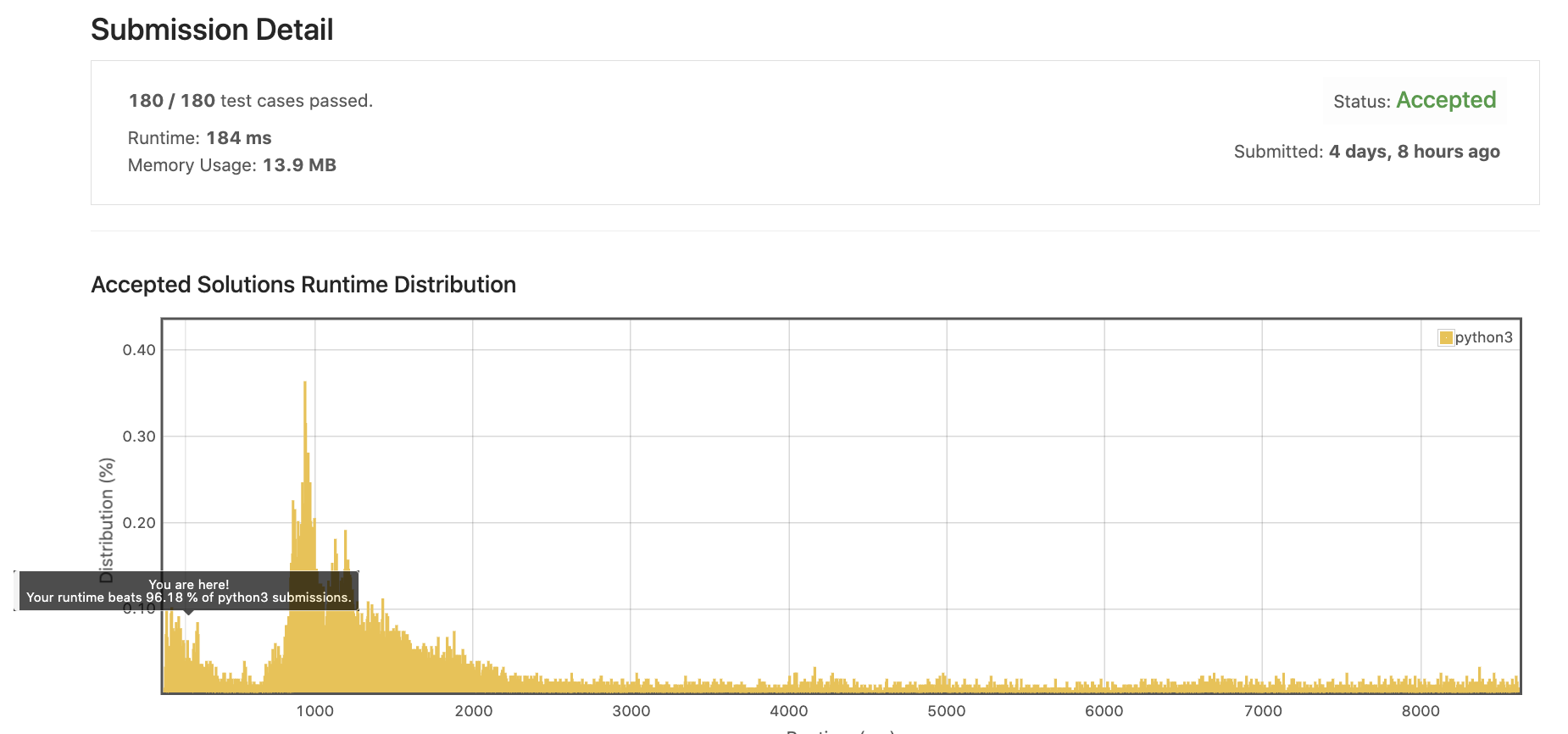

 

테스트케이스에 연속된 문자열이 많았는지 수행속도가 거의 1/10으로 줄었네요!

palindrome이 좌우 대칭이라는 생각에만 갇혀 이런 참신한 생각을 떠올리지 못했던게 아쉽습니다. ㅜㅜ